Problemas de funciones lineales
Da clic en el siguiente vínculo, para imprimir los problemas: https://drive.google.com/file/d/0B3869GFJaoVJTmpIN0wtV1lHSlk/view?usp=sharing
Sino puedes visualizarlos, puedes copiarlos a continuación.
1. Una compañía telefónica cobra una renta mensual de
$100 por 100 llamadas y posteriormente una tarifa de $1.50 por cada llamada
extra. ¿Cuál de las siguientes expresiones algebraicas refleja mejor la
situación de cobro mensual?
A)
y= 100 +
1.5x B) y= 100 + 50x C) y= 100 + 150x D) y= 100 + 50(1.5x)
2. Las siguientes gráficas representan el llenado de
cuatro tinacos de 300 litros cada uno, que se encontraban previamente llenos
hasta la mitad. Si se llenaron con llaves que proporcionan distinta cantidad de
agua, ¿cuál de ellos se llenó más rápido?
3. Un
taxista cobra $5.00 en el momento en que te subes, después de 15 minutos de
viaje te cobra $32.00, como se representa en la gráfica:
¿Cuánto te
cobrará si estas por 41 minutos estas viajando en el taxi?
4. La
siguiente gráfica muestra cómo varió la temperaura ambiental un día de otoño en
la ciudad de México. ¿Durante qué intervalo de tiempo la temperatura aumentó más
rápidamente?
A) De las
07:00 a las 09:00 horas
B) De las
13:00 a las 15:00 horas
C) De las
15:00 a las 17:00 horas
D) De las
17:00 a las 19:00 horas
5. Observa la siguientes ecuaciones:
¿A cuál familia de rectas representa?
6. ¿Cuál
de las siguientes gráficas representa la variación del perímetro de una
circunferencia con relación a su radio?
7. La siguiente
gráfica nos representa la producción de arreglos de una florería y los días en
que se producen. De acuerdo con la gráfica y con las mismas condiciones de
producción, ¿cuántos arreglos se producen en 25 días?
8. Juan construyó una cerca en cierto tiempo y
realizó la siguiente tabla para registrar su avance día a día.
¿Cuál de
las siguientes gráficas representa el avance de la construcción día a día de
acuerdo con la tabla que hizo Juan?
9. Observa
la siguiente gráfica que representa la altitud y el tiempo en que desciende un
paracaidista que se lanza desde un avión ubicado a una altura de 3 000 metros.
¿En cuál
de los siguientes intervalos de tiempo el paracaidista descenndió a mayor
velocidad desde su lanzamiento del avión?
A)
0 a 40
segundos B) 60 a 100 segundos C) 120 a 160 segundos D)180 a 260 segundos
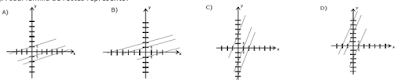
10. Encuentra la función que corresponde a cada
gráfica que se muestra abajo. Las funciones
son: a) y = 5x – 3, b) y = 5x + 3, c) y=
5x, d) y= 5x + 2. Coloca delante del
número de la gráfica el inciso que le corresponde.
11. Una
fábrica de lápices tiene una producción mínima de 1500 piezas por día. En las
sigueintes gráficas se muestra la producción de 4 semanas diferentes. ¿En cuál
de ellas se realizó la menor producción en el mayor tiempo?
12. Josué
llenó una pileta con una manguera que arroja 2 litros por segundo, y registró
el tiempo de llenado en una gráfica. ¿Qué forma tendrá la gráfica?
13. Del
año 1990 a 2001 el número de alumnos que egresaron de nivel licenciatura fue
como se muestra en la siguiente gráfica:
De acuerdo con sus datos, ¿en qué periodo egresaron más
estudiantes?
A) De 1991 a
1993 B) De
1993 a 1995 C) De 1996 a 1998 D) De
1998 a 2001
A) El auto
recorre una distancia constante cada cierto tiempo
B) Al inicio
de su recorrido el auto se encuentra ubicado en el punto A.
C) El auto se
encontraba al inicio de su recorrido a 100 metros del punto A.
D)
Al final de su recorrido el auto terminó a menos de 1 100 metros del punto
A.
15.
Observa la siguiente gráfica que hizo Roberto para su tarea:¿Cuál de las
sigueintes opciones identifica a la familia de rectas que graficó Roberto?
A) y= 3x + 5
|
B) y= - 3x + 5
|
C) y= 5x + 3
|
D) y= 3x + 5
|
y= 3x
|
y= - 3x
|
y= x + 3
|
y= x + 5
|
y = 3x - 10
|
y = - 3x - 10
|
y = 10x + 3
|
y = 10x + 5
|